Кривые безразличия и бюджетные ограничения
Любая точка, лежащая выше и правее кривой (например, К) будет предпочтительнее, чем любая точка кривой. Точка, лежащая ниже кривой, принесет меньше удовлетворения (например, N).
Рассмотри свойства кривых безразличия:
1. Кривая имеет отрицательный наклон, т.к. при постоянной полезности набора из двух товаров, чтобы увеличить количество одного товара в наборе, нужно отказаться от другого товара.
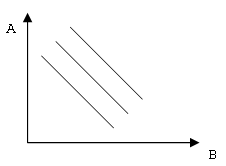
2. Через любую точку в графическом пространстве можно провести соответствующую кривую безразличия. Так мы получим карту кривых безразличия:
3. Любая кривая безразличия, лежащая выше и правее другой представляет собой высокий уровень полезности.
4. Две кривые безразличия не могут пересекаться и касаться друг друга.
5. Форма кривой – она вогнута по отношению к началу координат. Это объясняется сокращением предельной нормы замещения (MRS):
![]() .
.
MRS — это количество одного товара, от которого мы готовы отказаться ради увеличения потребления другого товара. Знак «–» перед дробью необходим, чтобы значение MRS было положительно, т.к. ΔY отрицательно.
Есть два особых случая конфигурации кривых безразличия:
1. Товары А и В — абсолютные субституты. Тогда кривые безразличия имеют вид: